Nonlinear Cancer Treatment Model
Project Overview
Evaluation of existing nonlinear models that simulated dynamics of cancer growth and treatment. Fixed point and bifurcation analysis conducted for untreated and chemotherapeutically treated tumors.
Project Objective
To create a predictive model for cancer progression under various treatment regimens, aiding in the personalization of therapy.
Specifications
- Selected cancer model must be multidimensional
- Must perform stability and bifurcation analysis
Technical Process
1. Literature Review
Developed an understanding of tumor growth dynamics through review of De Aruajo et Al’s work entitled An Analysis of a Mathematical Model Describing the Growth of a Tumor Treated with Chemotherapy.
2. Assigned Values to Parameters
Established scaled values for each of the model’s parameters using reasonable quantities based on the work by Aruajo et al.
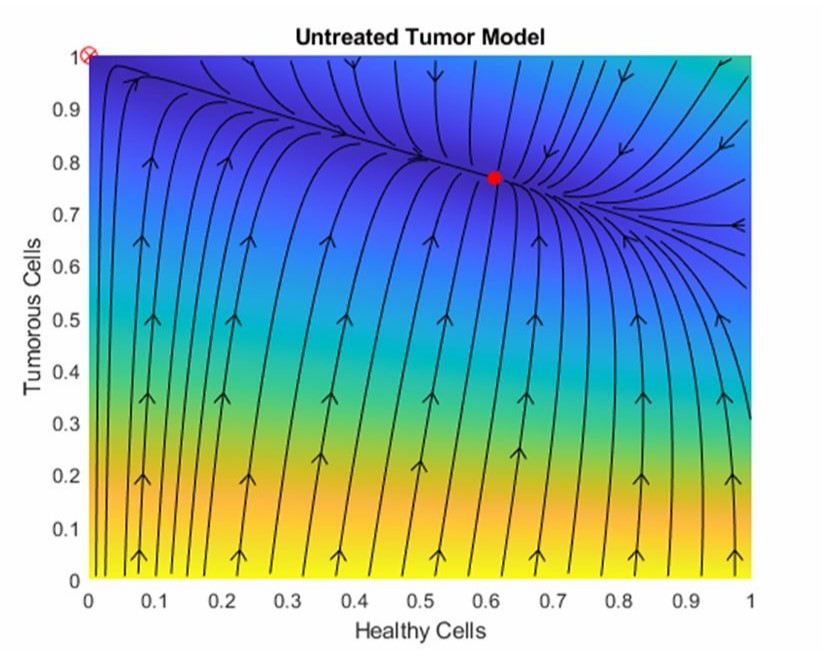
3. Evaluated Fixed Points for Untreated Model
Converted the cancer model to an untreated model, removing drug concentration and yielding a two dimensional model. Solved new model for fixed points and null clines by setting 2nd order terms equal to zero which found 2 fixed points in the quadrant of interest. Categorized fixed points by calculating Jacobian and finding traces. Found location by calculating eigenvalues for each fixed point.
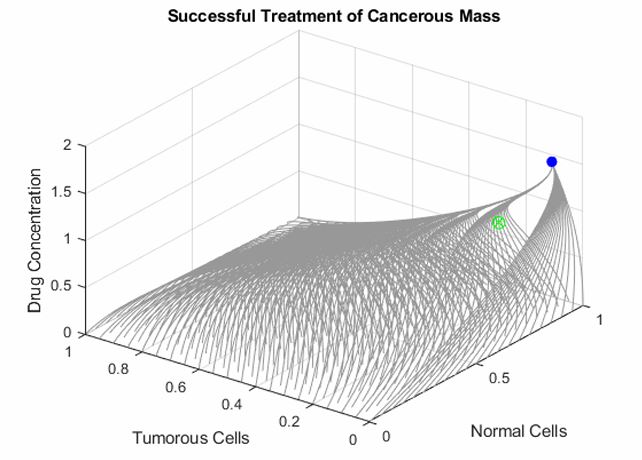
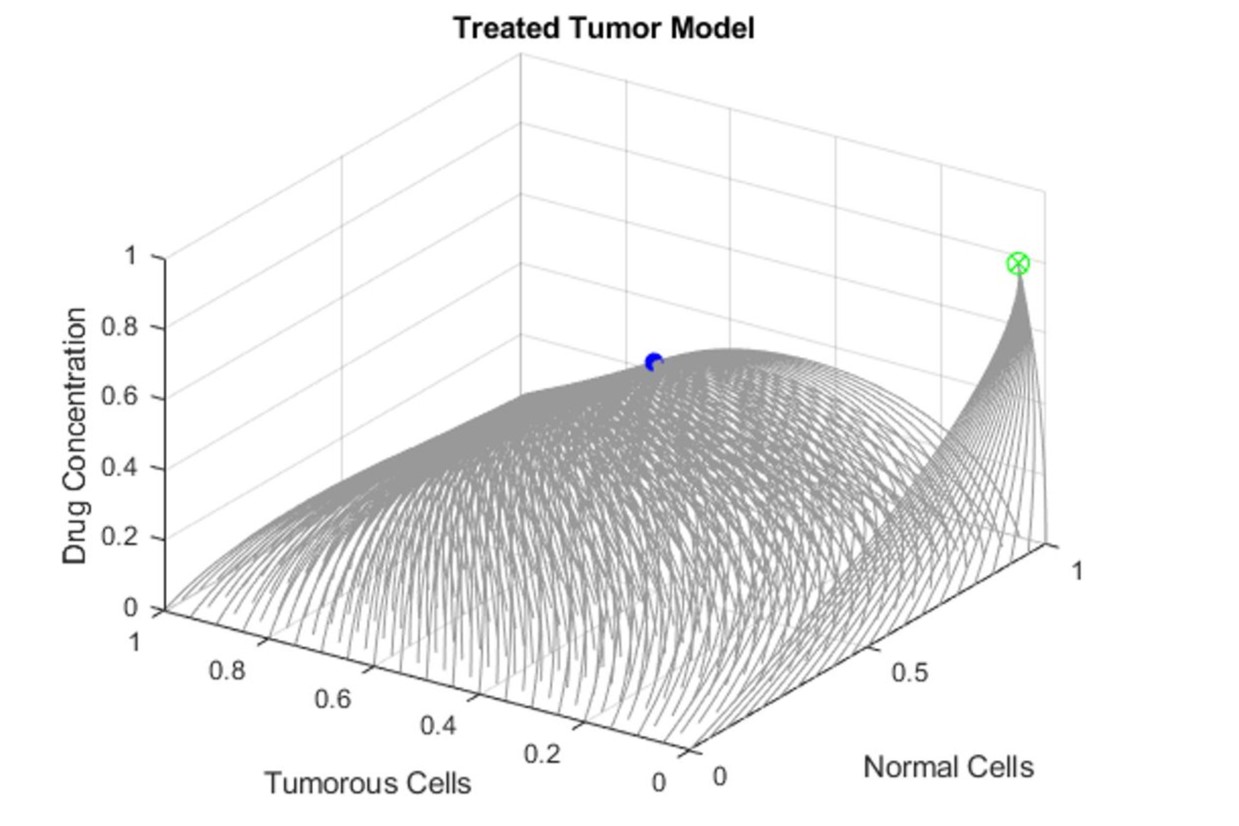
4. Solved Fixed Points for Treated Model
Solved fixed points and location MATLAB using previously established scaled parameters.
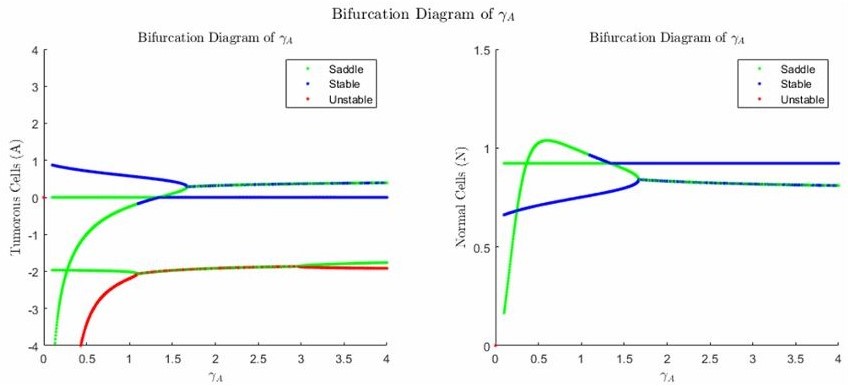
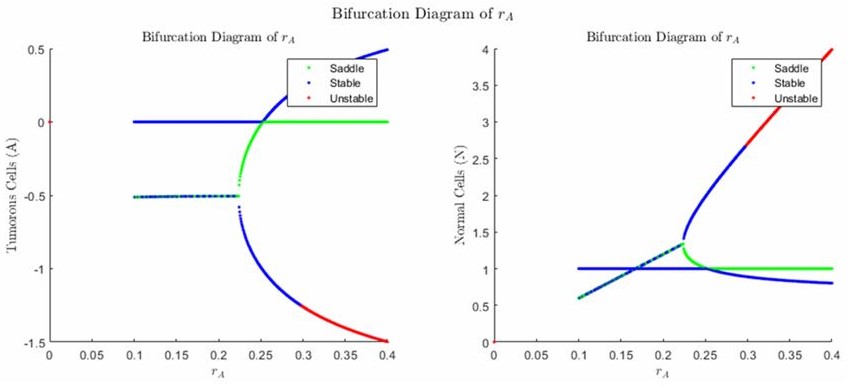
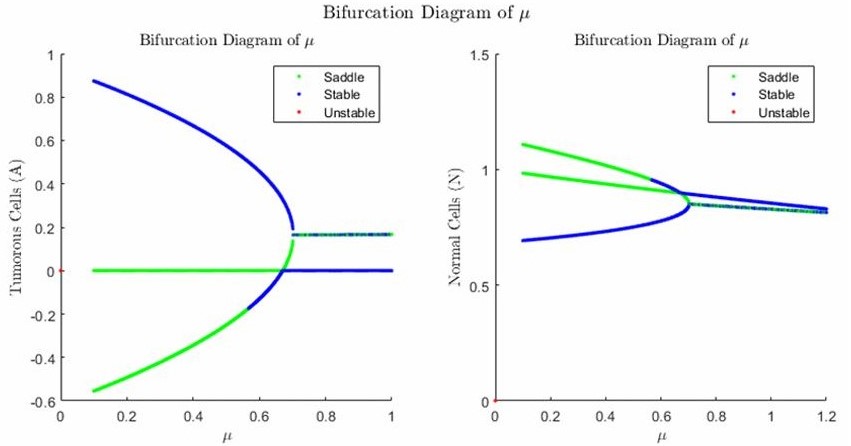
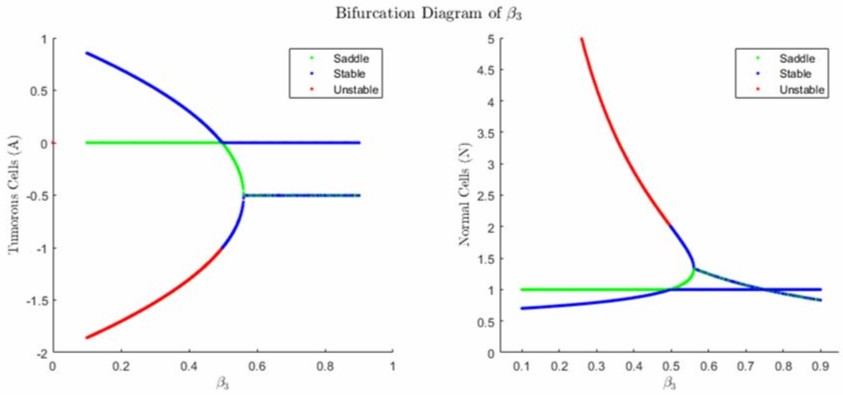
5. Performed Bifurcation Analysis for Treated Model
Bifurcation analysis performed on fixed points for numerous parameters including: Tissue Interaction Parameter, Tumor Cell Influx Rate, Absorption/Deactivation Rate and Drug Infusion Rate. Solved critical values of each bifurcation study.
Activation/Deactivation Rate Bifurcation Cancer Cell Influx Rate Bifurcation Infusion Rate Bifurcation Tissue Interaction Parameter Bifurcation 6. Model Behavior Discussion
Discussed behavior of cancer model under varying parameters including bifurcation studies and fixed points. highlighted value of using numerical models to inform treatment decisions and improve efficacy.
Outcome and Impact
- Utilized evaluation techniques to perform stability and bifurcation analysis on nonlinear systems.
- Reinforced the importance of using using numerical models to inform decision making within medical treatment and engineering.